長方形鏡筒 内の 点光源

◎ 中性子のための“ガイド管”を間近で見る機会がありました。長方形の筒に鏡が内張りされているものです。

言ってみれば、９０°Kaleidoscope（万華鏡）です。

◎ この中に点光源を入れたら　どんな具合に見えるのか

興味が湧いたので、少し考えて見ました。

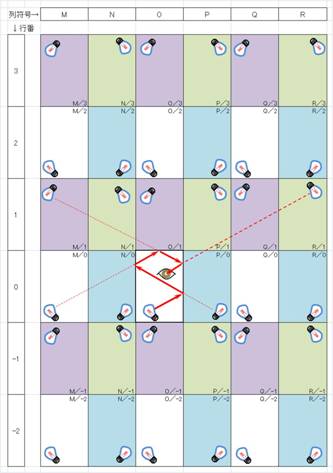
◎ 鏡筒（図の太枠）を覗くと、鏡の枠縁が向かい合った

ほかの鏡に映って、無数の格子が見えます。

筒の中にランプを置くと、左右反転・上下反転などを

繰り返して、無数のランプの像が見えます。

（着色は同じパターンを識別するために施しました）

◎ 例えば、列／行＝R／１の像を見ているときは、

その視線（太い破線）は　鏡の枠線を４回 横断

しています。

R／１の像はM／１の像の右鏡による左右反転像

M／１の像はM／０の像の上鏡による上下反転像

M／０の像はP／０の像の左鏡による左右反転像

P／０の像はＯ／０のランプの右鏡による左右反転像

ですから、眼は細い破線を順に追って見ていることに

なります。

即ち、ランプを発した光は矢印線の経路を辿って

眼に届いているわけです。

◎ さて、この時に光の強さはどうなるでしょう？

右下の図を見てください。

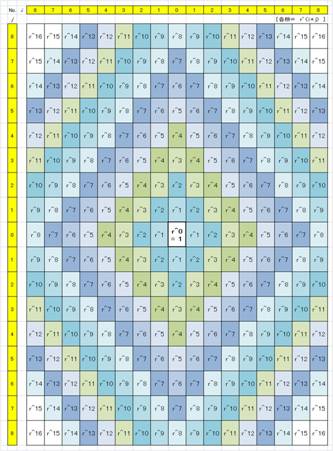
今度は、列(ｉ)、行(ｊ) ともに数字にしました。

列―行＝０−０(ｾﾞﾛ-ｾﾞﾛ)のところが光源です。

◎ 光源から 列―行＝ｉ−ｊ の像までを直線で結ぶと、

鏡枠像の仕切り線を、横方向にｉ回、縦方向にｊ回

横断しています。

◎ 反射率＝ｒ とすると、列―行＝ｉ−ｊ の枡の中の

ランプの像は、ｉ＋ｊ回の反射を繰り返しています

から、光の強さは、ｒの（ｉ＋ｊ）乗 ＝ ｒ^(ｉ＋ｊ)

となるわけです。

右の図は、そのことを表しています。

同じ値が　ひし形に並んでいますね。

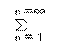◎ これらの値を無限のはてまで加え合わせたら、どうなるでしょう？　これは次の式で表せます。

　　　 　　　　(4ｎ×r ⁿ) ＝ ４*ｒ／（1−ｒ）^２

これに、中央の光源自体の強度（＝１）も加えあわせると、

４*ｒ／（1−ｒ）^２ ＋１＝（1＋ｒ）^２／（1−ｒ）^２

例えば　ｒ＝0.85と仮定すると、この値は　152.111・・・　と大変大きな値になります。

◎ だけど、光は　この値の分　まるまるが増幅して見えるわけじゃありません。

写像が　眼と光源を結ぶ線（軸線）から横にずれていることで、次のような目減りが生じます。

・ 眼と写像の距離が長くなるので、距離の二乗に反比例して見かけの光度が減る。

・ 眼に入ってくる角度(仰角：θ)が増え、cos(θ)に比例して見かけの光度が減る。

このことを演繹的な計算式で表すのは難しいので、

一定の仮定のもとで試算した例を紹介します。

仮定：

・ 眼と光源の距離＝１ｍ，2ｍ，5ｍ，10ｍ，100ｍ

・ 鏡筒の内法の高さ＝1／16 ｍ（＝62.5ｍｍ）

・ 鏡筒の内法の高さ＝1／25 ｍ（＝40.0ｍｍ）

・ 反射率　ｒ＝0.85

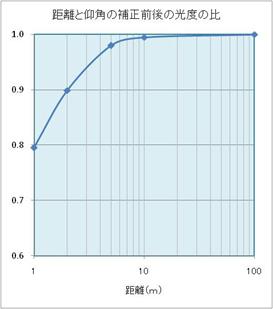
結果は、右図のように　距離＝１ｍ では 80%弱に目減りします。

（補正前の光度とは、すべての写像を軸線上の光源の位置に

　集めたと仮定した“見かけ上の光度”です）

◎ 上の図は、遠いほど照度が高くなると

言うわけじゃありません。

遠いほど斜めの度合いが減るので、

補正前の光度と補正後の光度の比

（いわば効率）が 好くなるという

だけです。

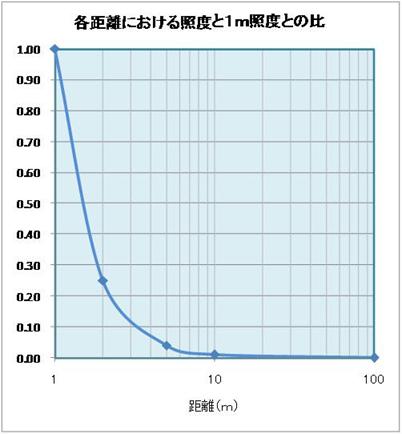
◎ 距離＝１ｍで補正後の光度に基づく

照度を＝１として、

各々の距離における補正後の光度に

基づく照度の比を表すと、

左の図のようになります。

◎ 距離＝１ｍの例について、左右の写像をすべて平行移動して中央の縦断面のうえに集めたと仮定すると、

その見かけの光度は下の左の図のようになります。

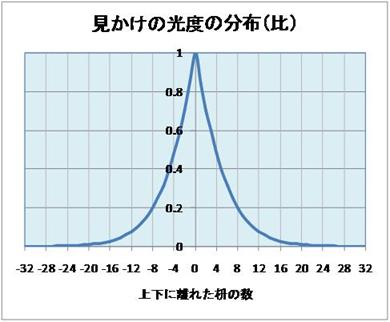
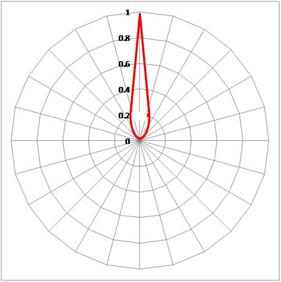
例えば、±８桝目（１ｍの半分縦ずれ、θ＝27°）で２０％、±16桝目（１ｍ縦ずれ、θ＝45°）で

0.3％、32桝目（１ｍの2倍縦ずれ、θ＝63°）で0.05％≒ゼロ　ですから、これをレーダーチャート

に表すと、右上の図のようになります。

各方向の累計でみると、5 〜6桝目（θ＝17 〜20°）までを覗けば、５０％以上の光を集めることが

出来そうです。

☆ 閑話休題 ☆

Kaleidoscope（万華鏡）は、英国の王立協会のコプリメダルまで受賞した　光学分野では多大の功績が

ある　Sir David Brewster （ディヴィッド・ブリュースター卿　1781 〜1868年）が再発見したもので、

氏は、灯台の光を遠くに届けるための研究もしていたそうです。［Wｉｋｉｐｅｄｉａ などより引用］

長方形鏡筒は　集光能力や方向整列能力が大変高いもので、

灯台の研究の中からKaleidoscope（氏の造語だそうです）の特許などが生まれてきたという

エピソードも　「なるほど！」と思わせるところがありますね。

　　長方形鏡筒の見え方の話はもう少し続きます・・・

◎ さて、冒頭のイラストは軸直角断面ですが、軸を面内に含む鉛直断面で見るとどうなるでしょう。

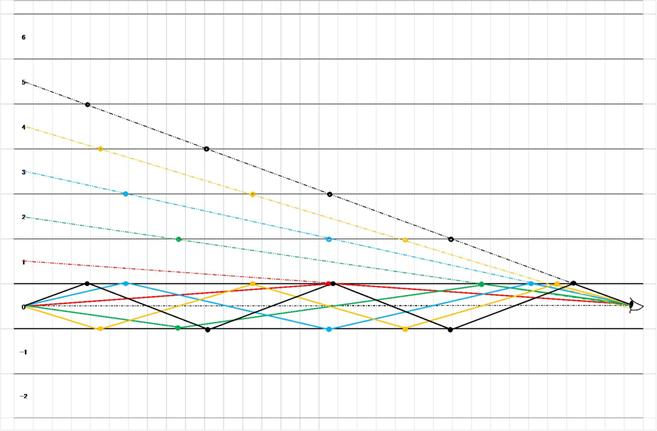
この図は、仰ぐように　1桝目から5桝目までの各々の写像を眺めた視線を表しています。

各視線（破線）が桝目の境界線を横断した回数だけ　鏡筒の上下の鏡面で反射を繰り返しています。

例えば、５桝目の像を見ようとしている時に　もし、鏡筒が両端の黒い点よりも短いとすると、

その視線の角度では光源を反射させることが出来ないので、像は見ることができません。

◎ ｎ番目までの像を見るためには、下の図の条件を満たさないといけないわけです。

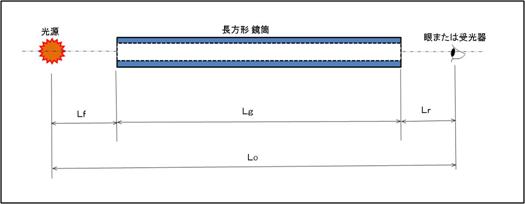
Ｌｆ　≪　Ｌｏ／２ｎ　　　　　　　　　　　　　　Ｌｒ　≪　Ｌｏ／２ｎ

したがって　当然のことですが、　Ｌｇ　≫　Ｌo*（ｎ−１）／ｎ　ですね。

◎ これまで　お話してきたことは、光が 少なくとも　立体角＝２πステラジアン（半球）の範囲内に

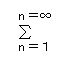均等な光束を発光しているような光源を対象にしています。

(4ｎ×rⁿ) ＋1＝ ４*ｒ／（1−ｒ）^２＋1の式で、無限大まで加算してよいのは、

軸線と直角の方向にも　均一な発光があることが前提です。

例えば、発光立体角が小さくて6桝目の仰角に相当する角度以上には光束が期待できないとか、

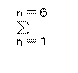あるいは、鏡筒が短くて7桝目以上の写像は眼に入らない場合は、

　　　 (4ｎ×rⁿ) ＋１　としなければならず、例えば ｒ＝0.85 の場合のこの値は、約43.83ですから、

無限大まで加算した　152.11 とは大幅にちがいます。

◎ 別の角度から　もう一つ考えて見ます。

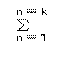例えば、一つの鏡筒で光源の光を集め、そのうしろに 少し離して もう一つの鏡筒を置いた場合に、

2番目の鏡筒に入ってきた光は方向が軸線の向きにほぼ揃えられているので、　 　　　　(4ｎ×rⁿ) 　

の式はもう使えません。

2番目の鏡筒は、ボウリングのガターのように　軸線から外れた方向の光線を整列する能力はあっても、

光を集めて光量を増幅する働きはもうしなくなるでしょう。

／／　なにか尻切れトンボですが、お話は一旦ここで終わります。永らく有難うございました。　／／

チキウ岬灯台（北海道室蘭市）［Wｉｋｉｐｅｄｉａ の“灯台”のページから引用］

この岬に立つと、なんとなく地球を眺めている気持ちになりますよ ・・・・・・・・